Algorithm - Max Sub Array Sum of Circular Array

Given a circular array C of integers represented by A, find the maximum possible sum of a non-empty subarray of C.

Here, a circular array means the end of the array connects to the beginning of the array. (Formally, C[i] = A[i] when 0 <= i < A.length, and C[i+A.length] = C[i] when i >= 0.)

Also, a subarray may only include each element of the fixed buffer A at most once. (Formally, for a subarray C[i], C[i+1], ..., C[j], there does not exist i <= k1, k2 <= j with k1 % A.length = k2 % A.length.)

Solution

A max sum subArray has two scenario.

dp approach

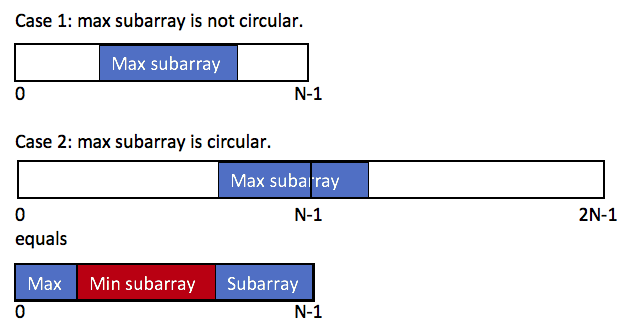
By iterating through the array A, if dp[j] represents the max sum of sub-array ending at j, them dp[j+1] would be dp[j] + max(A[j+1], 0)

because there are only two scenarios for dp[j+1] if we already know dp[j]

Scenario 1. A[j+1] > 0 then by including A[j+1] our new sum is larger than the previous sum

Scenario 2. A[j+1] <= 0 then by including A[j+1] our new is less or equal to the previous sum

class Solution:
    def maxSubarraySumCircular(self, A):
        total, maxSum, curMax, minSum, curMin = 0, A[0], 0, A[0], 0
        for a in A:
            curMax = max(curMax + a, a)
            maxSum = max(maxSum, curMax)
            curMin = min(curMin + a, a)
            minSum = min(minSum, curMin)
            total += a
        return max(maxSum, total - minSum) if maxSum > 0 else maxSum